Family 9 consists of the complementary rotational elements. Those elements are in turn divided into aileron rolls (Subfamilies 9.1 through 9.8), snap rolls (Subfamilies 9.9 and 9.10), and spins (Subfamilies 9.11 and 9.12). Solely through use of Aresti’s notation, without a single word spoken or written, we can tell the pilot exactly what kind of rotational element to fly and how much rotation to use.
The three new Aresti symbols we are now adding to your vocabulary are: curved arrows depicting aileron rolls; isosceles triangles indicating snap rolls; and right triangles symbolizing spins.
![]()
The aileron roll symbol is always drawn on a figure so as to be concave in the direction of flight. For snap rolls and spins,the symbol is drawn on the figure such that the short tail, or “flag,” at the triangle’s vertex points in the direction of flight.
A quick look in Family 9 will show that aileron rolls actually come in four varieties (Slow, 2-Point, 4-Point, and 8-Point); snap rolls in two varieties (Positive and Negative); and even spins have two types (Upright and Inverted). We must therefore have a way of modifying these three symbols to show the exact type of roll to fly and how much rotation to use in that element.
A plain arrow symbol, such as you see in Figure 3, represents a slow roll (Subfamily 9.1). Does using a ‘slow’ roll symbol mean we are asking the pilot to rotate the airplane at a very slow rate? No, the name “slow roll” comes from the early days of aerobatics when airplanes could snap roll at very much higher rates than they could using ailerons only. Modern, high-performance airplanes can rotate aileron rolls as fast as they can snap rolls, but the name has stuck and when we speak of a slow roll, we actually mean, “a roll with continuous rotation.” So, for example, a 1 1/2 slow roll means the aircraft rotates 540° degrees without stopping. The actual rate of the roll’s rotation is unspecified and immaterial.
Subfamilies 9.2, 9.4, and 9.8 are a subset of aileron rolls called ‘hesitation’ or ‘point’ rolls. Unlike slow rolls which have continuous rotation for the extent of their rotation, hesitation rolls do exactly that. They hesitate, or stop, a given number of times for each 360° of rotation. That is, 2-point rolls stop each 180° of rotation, 4-point rolls stop every 90° of rotation, and 8-point rolls stop every 45° of rotation.
How do we convey to the pilot that they should ‘hesitate’ their rolls? Simple. We put a number next to the arrowhead that defines the roll as 2, 4, or 8 point roll. Like this:
![]()
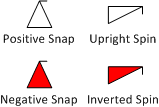
So arrows without numbers are slow rolls and arrows with numbers are hesitation rolls, but how do we differentiate the two types of snaps (positive and negative) and spins (upright and inverted)? In each case the symbol itself doesn’t change, but the triangles for the positive snap and upright spin are left unfilled, and the triangles for the negative snaps and inverted spins are filled in. Exactly as you learned earlier for negative (dashed) lines, the normal color used to fill these symbols is red, but whether they are red, black, or purple, doesn’t matter. The key to defining the rotational element’s type is whether they are filled in or not (Figure 5):
So now you understand how to notate the specific type of rotating element you require to be flown on a figure, but we are still left with letting the pilot know how many rotations to make within that element. As a quick aside, Family 9 rotation is always in multiples of 90°, but cannot be greater than 720° for a single element. Not every Family 9 subfamily has every possible rotation, either. For example there is never less than a half snap or less than a 1 turn spin.
For indicating the amount of rotation to use, the wonderful logic of the Aresti language shines through again. In fact, it’s so logical that rather than explain it and then show you examples, I’m going to show you examples of notating different rotations and ask if you can find the logic.
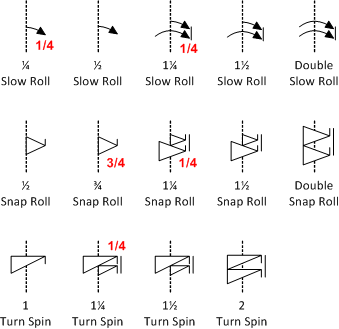
Figured it out? One symbol, be it aileron roll, snap roll, or spin equals one (360°) rotation. Half of a symbol (sidebar: another way to view a “half symbol” is that the arrow or triangle does not cross the line segment on which it is drawn) equals half (180°) a rotation. Couldn’t be easier, but what about rotations which are less than one-half or more than one turn?
That’s pretty straightforward as well. Fractions of continuous rotations (slow rolls, snaps, and spins) are shown as “¼” or “¾”. If there is less than one full rotation, but not exactly half, we still use a half symbol, but simply write the fractional rotation next to it. If there is more than one rotation, but less than two full rotations, we put a half symbol alongside a full symbol and join the two symbols with a linking line to show that the two symbols together represent a single roll. Again, we simply write the fraction “¼” or “¾” next to the linked symbols if the rotation is not exactly one and half (540°). Should the desired rotation be 720°, then we use two full symbols (each representing one full rotation) and join them with a linking line. All perfectly logical and consistent.
In the preceding paragraph I described how to notate fractions of continuous rotation. What if the rotation is not continuous, that is, what if the rotational element is a 2, 4, or 8-point hesitation roll? For those we use a slightly different notation. The logic of using a half, whole, or two linked symbols still applies, but instead of using fractions like “¾”, we use a notation in the form AxB, where A is the number of roll segments to be flown, and B is the number of roll segments that would occur in 360° of roll. Single rotation hesitation rolls use the B notation only.
All hesitation rolls are notated exactly the same way, so I will use a 4-point roll to illustrate the use of the AxB notation:

Notice that even if a hesitation roll is exactly half a rotation or two full rotations, we still use the AxB notation. When verbalizing these rolls, the “x” is pronounced, “of.” Thus, a 2x4 roll would be spoken as “2 of 4”, a 6x4 roll as a “6 of 4” roll. Another way to visualize hesitation rolls is that the pilot is being asked to perform multiple partial rolls. For example, a single 2-point roll is two half rolls performed with a slight hesitation separating the half rolls. Therefore a 3x2 roll can be thought of as three half rolls each with a short hesitation separating them. A 3x4 roll is really three one-quarter rolls with a short stop separating them. You get the idea.
Well, that was quite a little side trip from learning how to drawn a complete figure, but of course you can’t draw a complete figure unless you understand the rotational elements which may or must be placed on that figure. Back to our 1.2.3.1 Catalogue figure.
The most basic way to turn this catalogue figure into a real-world figure is to ignore the optional vertical roll and add the simplest of all 180° attitude changing rolls, the 1/2 slow roll. That gives us a figure which looks like this:
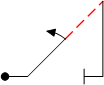
For Figure 8, the pilot would begin the figure flying left to right and exit to the left. What if we want the exit to the right? Looking back in the Catalogue at 1.2.3.1 (Figure 2 above) we see there is an optional vertical roll symbol. So let’s exercise that option and put a half slow roll on the vertical down line:
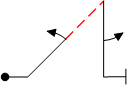
Look what happens to the exit line on the figure. It has reversed direction to show the effect of the half roll on the vertical line. Figure 9 highlights the point that in order to save many unnecessary pages the Catalogue only shows figures as entered left to right and with an exit direction that would result if none of the optional rolls were added. Of course, every figure in the Catalogue may also be flown right to left or starting/ending on the Y axis. The concept of indicating flight in a left to right or right to left direction on the X axis is easy enough to see with a drawing on a flat piece of paper, but how on earth do we represent an airplane flying directly at or away from the judges on a piece of paper?

